머신러닝으로 문제를 푸는 방법
머신러닝으로 문제를 풀 때, 푸는 방법을 나눌 수 있는데 결정은 직접 할 수 있다. 결정에 따라 모델의 설계 방법이 달라지게 된다. 어떤 문제는 회귀를 통해 푸는 것이 유리하고 어떤 문제는 분류를 통해 푸는 것이 유리하므로 신중히 결정해야 한다.
모든 문제를 풀기 위해서는 우선 입력값과 출력값이 정의되어야 한다.
- 회귀 (Regression)
출력값이 연속적인 문제를 풀 때 대개 회귀를 사용한다. 예를 들어, 나이, 키 등과 같이 연속적인 문제를 예측할 때 사용하게 되는 방법이 회귀이다.
- 분류 (Classification)
출력값이 비연속적인 문제를 풀 때 대개 분류를 사용한다. 예를 들어, Pass/Fail, 학점(A, B, C, D, F) 등과 같이 비연속적인 문제를 예측할 때 사용하게 되는 방법이 분류이다.
머신러닝에서의 학습 방법
머신러닝으로 학습을 시키는 방법은 크게 3가지로 나뉜다.
- 지도학습 (Supervised Learning)
정답 값을 알려주면서 모델을 학습시키는 형태이다. 회귀와 분류는 지도학습에 속한다. 정확도가 높은 경향이 있다. 그러나 정답 값이 필요하다는 단점이 있는데 (출력값을 가지고 있는 경우는 많지 않으니까), 이는 학습을 시키기 전에 입력값에 대한 출력값을 입력해주는 작업인 라벨링을 해주어야 한다는 단점으로 이어진다.
- 비지도학습 (Unsupervised Learning)
지도학습과 달리 정답 값을 모르는 상태에서 학습을 시키는 형태이다. 군집화(Clustering)는 비지도학습에 속한다. 당연하게도 지도학습에 비해 학습 방법이 어렵고, 학습 시간도 오래 걸린다는 단점이 있다. 그러나 정답 값이 없을 때 효과적으로 사용될 수 있다는 장점을 가진다. 예를 들어, 비슷한 음악끼리 분류해주는 것은 비지도학습으로 할 수 있다. (물론 장르에 대한 정보(정답 값)가 있으면 지도학습으로 이어질 수 있겠지만...?)
- 강화학습 (Reinforcement Learning)
주어진 데이터 없이 실행과 오류를 반복하도록 하는 학습 형태이다. 알파고가 대표적인 예로, 게임이나 실시간 처리에 자주 사용된다. 지도학습이나 비지도학습의 경우 모든 상황에 대비하는 데이터가 요구될 수도 있는 반면, 강화학습은 딥러닝이 등장하게 되면서 신경망을 적용하며 복잡한 문제에 대응할 수 있게 되었다.
선형회귀
'이 세상의 모든 법칙은 선형적이다' 라고 가정을 하고 문제에 접근하는 방법이다. 예를 들어, '공부 시간이 많을수록 높은 시험 점수를 받는다.' 등과 같은 가정을 하는 것이다. 선형 모델(가설)은 수식 H(x) = Wx + b 와 같은 형태로 표현할 수 있다.
지도학습이기 때문에 데이터셋에는 입력값과 출력값이 모두 존재하고, 각각을 x축과 y축이라 생각한다면 점들이 찍히게 될 것이다. 그 점들을 모두 지날 수는 없겠지만 점들과의 거리(MSE: Mean Squared Error, Cost Function)가 가장 작은 선 하나를 뽑아낸다. 그 선이 가장 정확하게 예측한 선이 된다.
물론, 머신러닝은 1차 함수가 아닌 더 고차원 함수를 사용하게 되는 경우가 많지만 원리는 똑같다. 데이터셋을 보고, 가설을 세운 후, 그에 대한 손실 함수를 정의하는 것이 우리가 해야하는 일이다.
다중선형회귀
선형회귀와 동일하되 입력값이 여러 개라고 생각하면 된다. 수식 H(x1, x2, ..., xn) = W1x1 + W2x2 + ... + Wnxn + b 와 같은 형태로 표현할 수 있다.
경사하강법 (Gradient Descent Method)
우리가 해야하는 일 중 하나인 손실 함수를 정의할 때 사용된다. 우리는 손실 함수를 최소화(Optimize)해야한다. 다음 그림을 보자.

우리가 세운 가설인 H(x) = Wx + b 에서 W에 따른 손실 함수를 그린 것이다. 우리는 손실 함수를 최소화해야하기 때문에 cost function이 최소가 되었을 때의 W 값을 찾아내야한다.

위 그림과 같이 초기 점부터 한 스텝 한 스텝씩 거리를 옮겨가며 검사를 해보면서 cost function이 최소가 될 때를 찾는 데, 그 스텝 거리를 Learning Rate라고 한다. 즉, Learning Rate가 크면 한 번에 많은 점을 움직일 수 있겠지만 Learning Rate가 작으면 한 번에 조금씩만 움직인다.

위 그림과 같이 Learning Rate가 너무 작은 경우에는 한 번에 너무 조금씩만 움직이기 때문에 cost function의 최소값을 찾는 데에 시간이 오래걸려 학습 시간이 오래 걸릴 수도 있다. 그렇다고 해서 Learning Rate가 크다고 무조건 좋은 것은 아니다.

위 그림과 같이 Learning Rate가 너무 큰 경우에는 우리가 찾으려는 cost function의 최소값을 그냥 지나쳐버릴 수도 있다. 최악의 경우에는 발산하는 경우까지 이르를 수 있는데 이를 Overshooting 이라고 한다.
즉, Learning Rate를 적절하게 바꿔가면서 적절한 값을 선택하는 것은 중요하다. 실제로 손실 함수는 그림들과 같은 이차함수가 아닌 그릴 수도 없는, 고차원의, 복잡한 형태를 가졌기 때문에 더더욱 중요하다.
데이터 셋
- Training Set
모델을 학습시킬 때 사용되는 데이터로 모델의 성능에 영향을 주며 전체의 약 80%를 차지한다.
- Validation Set
모델의 성능을 검증하고 튜닝하는 지표로 사용되는 데이터로 라벨링이 되어있다. 학습 단계에서 사용되는 데이터지만 모델에게 보여지는 데이터는 아니므로 성능에 영향을 주지는 않는다.
- Test Set
실제 환경에서의 평가 데이터로 라벨링이 되어있지 않은 순수 데이터다.
선형회귀 실습해보기 - Tensorflow 사용
import tensorflow as tf
tf.compat.v1.disable_eager_execution() # use ver.1
x_data = [[1, 1], [2, 2], [3, 3]]
y_data = [[10], [20], [30]]
X = tf.compat.v1.placeholder(tf.float32, shape=[None, 2]) # batch-size = None, input-size = 2
Y = tf.compat.v1.placeholder(tf.float32, shape=[None, 1]) # batch-size = None, output-size = 1
W = tf.Variable(tf.random.normal(shape=(2, 1)), name='W') # randomly initialize
b = tf.Variable(tf.random.normal(shape=(1,)), name='b') # randomly initialize[1, 1]이라는 input이 주어지면 [10]이라는 output이, [2, 2]이라는 input이 주어지면 [20]이라는 output이, [3, 3]이라는 input이 주어지면 [30]이라는 output이 나온다. tensorflow의 placeholder를 사용하여 input과 output의 자료형 및 크기를 정의해준다. 선형회귀를 사용할 것이기 때문에 모델을 H(x) = Wx + b 라고 가정하는데, W와 b의 초기값은 랜덤하게 생성해준다.
hypothesis = tf.matmul(X, W) + b # Liniear Regression
cost = tf.reduce_mean(tf.square(hypothesis - Y)) # cost function = MSE
optimizer = tf.compat.v1.train.GradientDescentOptimizer(learning_rate=0.01).minimize(cost) # optimizer = GDMH(x) = Wx + b 의 식을 정의해주고, cost function은 MSE(Mean Squared Error)를 사용할 것이고, optimizer는 GDM(Gradient Descent Method)을 사용할 것이라고 정의해준다. optimizer 정의 시, Learning Rate를 0.01로 설정하고, cost를 최소화하는 방향으로 갈 것임을 선언해준다.
with tf.compat.v1.Session() as sess:
sess.run(tf.compat.v1.global_variables_initializer()) # initialize all variables
for step in range(50): # repeat
c, W_, b_, _ = sess.run([cost, W, b, optimizer], feed_dict={X: x_data, Y: y_data})
print('Step: %2d\t loss: %.2f\t' % (step, c))
print(sess.run(hypothesis, feed_dict={X: [[4, 4]]}))50번의 학습을 하며 loss가 어떻게 변화하는지 살펴보자. 그리고 학습이 끝난 후에 input으로 [4, 4]가 들어오면 output이 뭐가 나올지 모델이 어떻게 예측했는지 살펴보자.

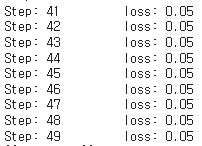
학습을 하면 할수록 loss가 줄어드는 것을 확인할 수 있었다.
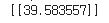
모델은 input이 [4, 4]일 경우 output으로는 [39.583557]이 나올 것이라고 예측하였다.
선형회귀 실습해보기 - Keras 사용
import numpy as np
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam, SGD
x_data = np.array([[1], [2], [3]])
y_data = np.array([[10], [20], [30]])
model = Sequential([
Dense(1) # only one output
])
model.compile(loss='mean_squared_error', optimizer=SGD(lr=0.1))
# loss(cost) function = MSE, optimizer = SGD(GDM), learning rate = 0.1
model.fit(x_data, y_data, epochs=100) # learn
y_pred = model.predict([[5]]) # predict
print(y_pred)Keras를 사용하게 되면 훨씬 짧은 코드로 구성할 수 있다. 내용이나 요구하는 조건은 위의 Tensorflow를 이용한 실습과 동일하다. 학습 중의 loss 변화 및 예측 결과를 살펴보자.


학습을 하면 할수록 loss가 줄어드는 것을 확인할 수 있다.
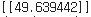
모델의 예측 결과이다.
선형회귀 실습해보기 with Kaggle - Advertising Dataset | Kaggle
우선, csv 파일을 읽어보자. 맨 위 5개의 데이터만을 출력해보자.
import pandas as pd
df = pd.read_csv('advertising.csv')
df.head(5)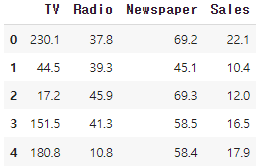
TV, Radio, Newspaper, Sales라는 column들로 이루어진 것을 확인할 수 있다.
위의 5개만 출력을 해봤지, 실제 크기가 얼마나 될지는 아직 알 수 없다. 실제 크기를 출력해보자.
print(df.shape)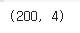
4개의 column으로 이루어져있고 총 200개의 row가 존재하는 것을 알 수 있다.
이제 각각의 column들이 상관관계를 가지고 있지는 않은지 확인해보자. TV와 Sales, Radio와 Sales, Newspaper와 Sales의 상관관계를 그래프로 그려보자.
import seaborn as sns
sns.pairplot(df, x_vars=['TV', 'Newspaper', 'Radio'], y_vars=['Sales'], height=4)
# Sales를 결과값으로 사용 (Sales를 예측하고자 할 경우!)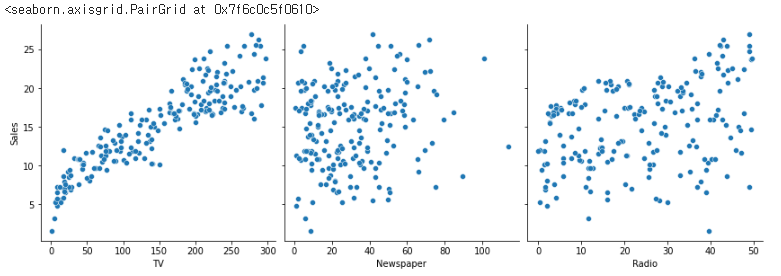
오... TV와 Sales가 선형적인 상관관계를 가지는 듯하다!!!!!!! 이제 데이터를 가공하고, train set 및 test set을 생성하여 모델을 학습시키고 테스트해보자.
from sklearn.model_selection import train_test_split
import numpy as np
x_data = np.array(df[['TV']], dtype=np.float32)
y_data = np.array(df['Sales'], dtype=np.float32)
x_data = x_data.reshape((-1, 1))
y_data = y_data.reshape((-1, 1))
x_train, x_val, y_train, y_val = train_test_split(x_data, y_data, test_size=0.2, random_state=201802118)위는 데이터를 가공하고 train, test set을 생성하는 코드이다.
model = Sequential([
Dense(1)
])
model.compile(loss='mean_squared_error', optimizer=Adam(lr=0.1))
model.fit(
x_train,
y_train,
validation_data=(x_val, y_val),
epochs=100
)모델을 학습시킨다. 이번에도 손실 함수로 MSE를, Optimizer로 Adam을 사용하고 Learning Rate는 0.1로 설정해주었다.

결과를 출력해보자.
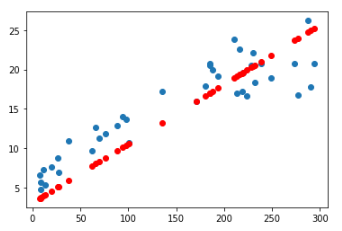
import matplotlib.pyplot as plt
y_pred = model.predict(x_val)
plt.scatter(x_val, y_val)
plt.scatter(x_val, y_pred, color='r')
plt.show()